Answer:
a) The heat input per cycle is 2857.143 joules.
b) The temperature of the low-temperature reservoir is 49.655 °C.
Step-by-step explanation:
a) The efficiency of the Carnot engine is defined by the following formula:
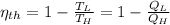 (1)
(1)
Where:
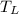 - Low temperature reservoir, in Kelvin.
- Low temperature reservoir, in Kelvin.
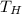 - High temperature reservoir, in Kelvin.
- High temperature reservoir, in Kelvin.
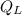 - Heat output, in joules.
- Heat output, in joules.
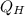 - Heat input, in joules.
- Heat input, in joules.
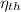 - Engine efficiency, no unit.
- Engine efficiency, no unit.
If we know that
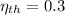 and
and
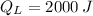 , the heat input of the Carnot engine is:
, the heat input of the Carnot engine is:
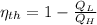
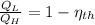
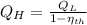
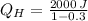
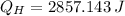
The heat input per cycle is 2857.143 joules.
b) If we know that
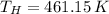 and
and
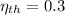 , then the temperature of the low-temperature reservoir:
, then the temperature of the low-temperature reservoir:
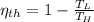
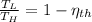
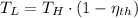
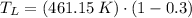
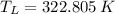
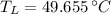
The temperature of the low-temperature reservoir is 49.655 °C.