Question

A Carnot engine with an efficiency of 30% operates with a high-temperature reservoir at 188oC and exhausts 2000 J of heat each cycle. What are (a) the heat input per cycle and (b) the Celcius temperature of the low-temperature reservoir

Answer 1

a) The heat input per cycle is 2857.143 joules.

b) The temperature of the low-temperature reservoir is 49.655 °C.

Step-by-step explanation:

a) The efficiency of the Carnot engine is defined by the following formula:

`\eta_(th) = 1-(T_(L))/(T_(H)) = 1 - (Q_(L))/(Q_(H))` (1)

Where:

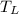`T_(L)` - Low temperature reservoir, in Kelvin.

`T_(H)` - High temperature reservoir, in Kelvin.

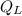`Q_(L)` - Heat output, in joules.

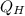`Q_(H)` - Heat input, in joules.

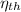`\eta_(th )` - Engine efficiency, no unit.

If we know that
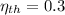`\eta_(th) = 0.3` and
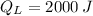`Q_(L) = 2000\,J`, the heat input of the Carnot engine is:

`\eta_(th) = 1 - (Q_(L))/(Q_(H))`

`(Q_(L))/(Q_(H)) = 1 - \eta_(th)`

`Q_(H) = (Q_(L))/(1-\eta_(th))`

`Q_(H) = (2000\,J)/(1-0.3)`

`Q_(H) = 2857.143\,J`

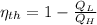
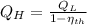
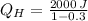
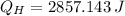
The heat input per cycle is 2857.143 joules.

b) If we know that
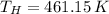`T_(H) = 461.15\,K` and
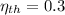`\eta_(th) = 0.3`, then the temperature of the low-temperature reservoir:

`\eta_(th) = 1 - (T_(L))/(T_(H))`

`(T_(L))/(T_(H)) = 1 - \eta_(th)`

`T_(L) = T_(H)\cdot (1-\eta_(th))`

`T_(L) = (461.15\,K)\cdot (1-0.3)`

`T_(L) = 322.805\,K`

`T_(L) = 49.655\,^(\circ)C`

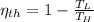
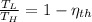
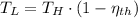
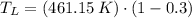
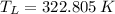
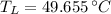
The temperature of the low-temperature reservoir is 49.655 °C.