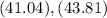Question

To estimate the mean length of rattlesnakes, 10 such snakes are randomly selected. Their lengths, in inches, are as follows: 40.2 43.1 45.4 44.5 39.5 40.2 41.0 41.6 43.1 44.9 Find a 90% confidence interval for the mean length of all rattlesnakes.

Answer 1

The confidence interval will be "41.04, 43.81".

Explanation:

Given that,

Sample size,

n = 10

Sample total,

423.5

Sample mean,

`\bar X =(423.5)/(10)`

`=42.35`

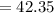
Sample variance,

`s = √(4.5894)`

`=2.1423`

`df=n-1`

`=9`

`t^*=18331`

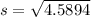
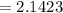
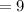
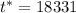
Now,

The margin of error will be:

⇒
`E=(s* t^*)/(√(n) )`

`=(2.1423* 1.8331)/(√(9) )`

`=(3.928)/(3 )`

`=1.309`

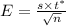
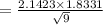
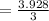
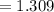
hence,

The 90% confidence level will be:

=
`(\bar X-E),(\bar X+E)`

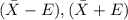
By substituting the values, we get

=
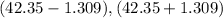
`(42.35-1.309),(42.35+1.309)`

=
`(41.04),(43.81)`