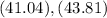Answer:
The confidence interval will be "41.04, 43.81".
Explanation:
Given that,
Sample size,
n = 10
Sample total,
423.5
Sample mean,
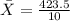
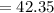
Sample variance,
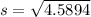
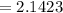
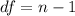
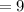
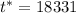
Now,
The margin of error will be:
⇒
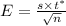
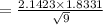
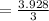
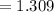
hence,
The 90% confidence level will be:
=
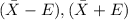
By substituting the values, we get
=
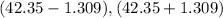
=