Question

Christine is going to use 20m of fencing to fence off a rectangular field to grow vegetables. She is considering three fields with lengths of 3m, 5m, and 6m.

Answer the questions below to find which of these fields would hold the most vegetables.

Answer 1

Answer:

6m field will hold most vegetables

Answer 2

The field with a length of 6m would hold the most vegetables. This conclusion is reached by maximizing the area of the rectangular field using the provided 20m of fencing. The calculated area for the 6m field is 24m², surpassing the areas of the 3m and 5m fields.

Explanation:

Christine's goal is to maximize the area of the rectangular field to grow the most vegetables. The area (A) of a rectangle is given by the formula A = length × width. In this case, the width can be calculated using the given information about the fencing.

The perimeter (P) of the rectangular field is equal to the total length of fencing and is given by the formula P = 2 × (length + width). Since the total length of fencing is 20m, we can set up an equation for the perimeter:

`\[20m = 2 × (6m + width)\]`

Solving for the width:

`\[10m = 6m + width\]`

`\[width = 4m\]`

Now that we have the width, we can calculate the area of the rectangular field:

`\[A = 6m × 4m = 24m^2\]`

We can repeat this process for the other field lengths:

1. For the 3m field, the width would be (7m) and the area would be
`\(3m × 7m = 21m^2\).`

2. For the 5m field, the width would be (5m) and the area would be
`\(5m × 5m = 25m^2\).`

Comparing the areas, we find that the field with a length of 6m has the largest area
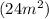`(24m^2)`, making it the optimal choice for growing the most vegetables with the given amount of fencing.