Question

The position of a particle at time tt is s(t)=t3+3t.s(t)=t3+3t. Compute the average velocity over the time interval [2,5][2,5] and estimate the instantaneous velocity at t=2.t=2. (Give your answers as whole numbers.)

Answer 1

(a) 42m/s

(b) 15m/s

Step-by-step explanation:

Given:

The position of a particle at time t

s(t) = t³ + 3t

(i) To compute the average velocity

Average velocity (
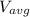`V_(avg)`) is given by the quotient of the change in position and change in time at a given interval of time. i.e

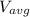`V_(avg)` = Δs / Δt

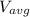`V_(avg)` = (s₂ - s₁) / (t₂ - t₁) --------------------(ii)

Given interval of time is [2,5]

Therefore,

t₁ = 2

t₂ = 5

s₁ = position of the particle at t₁.

This is found by substituting t = 2 into equation (i)

s₁ = (2)³ + 3(2)

s₁ = 8 + 6 = 14

s₂ = position of the particle at t₂

This is found by substituting t = 5 into equation (i)

s₂ = (5)³ + 3(5)

s₂ = 125 + 15 = 140

Now, substitute t₁, t₂, s₁ and s₂ into equation (ii) as follows;

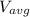`V_(avg)` = (s₂ - s₁) / (t₂ - t₁)

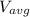`V_(avg)` = (140 - 14) / (5 - 2)

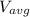`V_(avg)` = 126 / 3

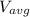`V_(avg)` = 42

Therefore, the average velocity is 42m/s

(ii) To compute the instantaneous velocity.

The instantaneous velocity is the velocity of the particle at a given instant in time.

The given instant in time is t = 2.

To get the instantaneous velocity (V), differentiate equation (i) with respect to t as follows;

V =
`(ds)/(dt)`

V =
`(d(t^3 + 3t))/(dt)`

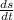
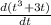
V = 3t² + 3

Now substitute the value of t = 2 into the above equation

V = 3(2)² + 3

V = 12 + 3

V = 15

Therefore, the instantaneous velocity at t = 2 is 15m/s