Question

The transportation department predicts that about 800,000 cars will be registered in a certain state by year 2012. Their license plates are made using and two letters followed by and three digits from 0 to 9. Will there be enough possible arrangements?

Answer 1

There won't be enough arrangement

Explanation:

Given

`Letters = 2`

`Digits= 3`

`Cars = 800000`

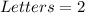
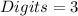
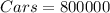
Required

Determine if the possible arrangement will be enough

The 2 letters can be selected from any of the 26 alphabets without restriction.

So, the selection of letters is:

`Letters = 26 * 26`

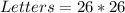
The 3 digits can be selected from any of the 10 digits without restriction.

So, the selection of digits is:

`Digits = 10*10*10`

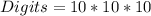
The total arrangement is:

`Total = Letters * Digits`

`Total = 26*26*10*10*10`

`Total = 676000`

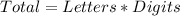
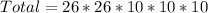
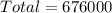
By comparison:

`Total < Cars`

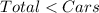
i.e.

`676000 < 800000`

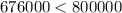
Hence, the arrangement will not be enough