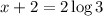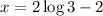Answer:
It depends on the equation.
If the bases are equal and the variables are only in the exponents, set the exponents equal.
If there are variables in the exponents, but you cannot set the bases equal, then use logarithms.
Example 1:

Here you have the same base on both sides. The variables are in the exponents. Set the exponents equal and solve for x.
2x + 5 = 9
2x = 4
x = 2
Example 2:
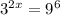
The bases are different, but you can make the bases equal using laws of exponents. Remember that 9 = 3^2.
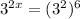
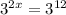
Now you have equal bases, so the exponents must be equal.
2x = 12
x = 6
Example 3:
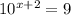
Here you can't make the bases equal, so you take the log of both sides and use laws of logs.
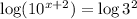
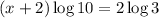
Recall that: