Answer:
i know there's a lot of explanation. but it helps u for sure :)
Explanation:
1)
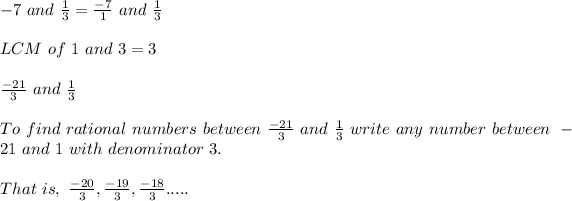
2)
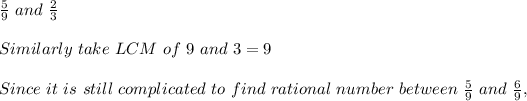

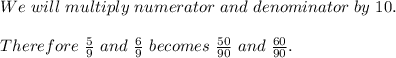
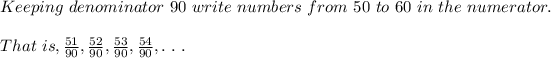
3)
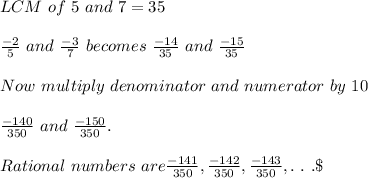
Tip :
1. Make the denominator same.
2. Multiply numerator and denominator by 10 , 100 or 1000
3. Just write the natural numbers between the 2 numerators keeping denominator same.