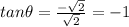Answer:
Explanation:
Since our interval is given as it is, we are in QIII. That interval is equivalent to 270 degrees to 360 degrees, which is QIII. If we draw this right triangle in QIII and label it accordingly, the side adjacent to the reference angle is sqrt2 and the hypotenuse is 2. We know this because the cosine ratio is defined as the side adjacent to the reference angle over the hypotenuse of the right triangle. That means that we have to find the missing side in order to determine the other 2 main trig ratios. Using Pythagorean's Theorem, we have
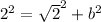 and
and
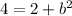 so
so
 . But since it is for a value that, in QIII is negative, it is
. But since it is for a value that, in QIII is negative, it is
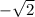
Now we can find the sin and tan of that reference angle. Sin is defined as the side opposite the reference angle over the hypotenuse, so
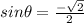 and tan, which is defined as side opposite the reference angle over the side adjacent to the reference angle, then
and tan, which is defined as side opposite the reference angle over the side adjacent to the reference angle, then