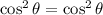Answer:
See Below.
Explanation:
11)
We have:
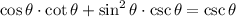
Rewrite:
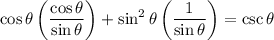
Multiply:
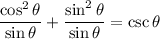
Combine:
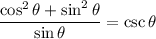
According to the Pythagorean Identity, sin²θ + cos²θ = 1. Hence:
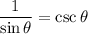
Simplify:
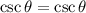
12)
We have:
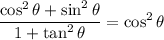
Pythagorean Identity:
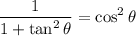
From the Pythagorean Identity, if we divide both sides by cos²θ, we acquire that tan²θ + 1 = sec²θ. Hence:
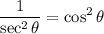
Simplify:
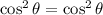
13)
We have:
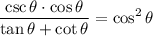
Rewrite:
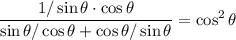
Multiply both top and bottom by cosθsinθ. Hence:
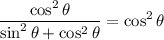
By the Pythagorean Identity:
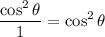
Simplify: