Question

In the Salk vaccine field trial, 400,000 children were part of a randomized controlled double-blind experiment. Just about half of them were assigned at random to the vaccine group, and the other half to the placebo.16 In the vaccine group, there were 57 cases of polio, compared to 142 in the placebo group. Is this difference due to chance? If not, what explains it?

Answer 1

Explanation:

From the given information:

The number of children that were randomly allocated to each vaccination group; n₁ = 200,000

No of polio cases X₁ = 57

Now, in the vaccine group:

the proportion of polio cases is:

`\hat p_1 = (57)/(200000)`

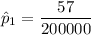
= 0.000285

The number of children that were randomly allocated to the placebo group, n₂ = 200,000

No of polio cases X₂ = 142

In the placebo group

the proportion of polio cases is:

`\hat p_2 = (142)/(200000)`

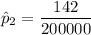
Null and alternative hypothesis is computed as follows:

H₀: There is no difference in the proportions of polio cases between both groups.

H₁: There is a difference in the proportions of polio cases between both groups.

Let assume that the level of significance ∝ = 0.05

The test statistic can be computed as:

`Z = \frac{\hat p_1-\hat p_2}{\sqrt{(\hat p_1 \hat q_1)/(n_1)+ (\hat p_2 \hat q_2)/(n_2)}}`

`Z = \frac{0.000285-0.000710}{\sqrt{(0.000285(1-0.000285))/(200000)+ (0.000710(1-0.000710))/(200000)}}`

`Z = \frac{-4.25* 10^(-4)}{\sqrt{(0.000285(0.999715))/(200000)+ (0.000710(0.99929))/(200000)}}`

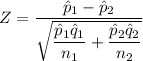
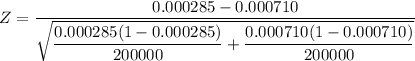
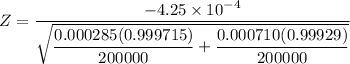
Z = - 6.03

P-value = 2P(Z < -6.03)

From the Z - tables

P-value = 2 × 0.0000

= 0.000

We reject the H₀ provided that P-value is very less.

Therefore, we may conclude that there is a difference in the proportions of polio cases between the vaccine group and placebo group not due to chance.