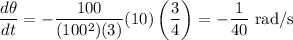Answer:
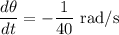
Explanation:
We can model the situation with the diagram below.
The relationship between the angle between the string and the horizontal can be modeled by:
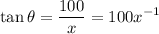
Differentiate the equation with respect to time t:
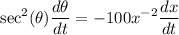
When 200 ft of string have been left out, a = 200.
By the Pythagorean Theorem:
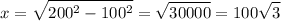
Then it follows that:
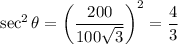
And since the kite moves horizontally at a speed of 10 ft/s, dx/dt = 10.
Substitute:
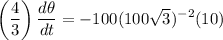
So: