Given:
There are two consecutive odd integers such that the square of the first added to 3 times the second, is 24.
To find:
Part a: Define the variables.
Part b: Set up an equations that can be solved to find the integers.
Part c: Find the integers.
Solution:
Part a:
Let x be the first odd integers. Then next consecutive odd integer is
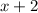 , because the difference between two consecutive odd integers is 2.
, because the difference between two consecutive odd integers is 2.
Part b:
Square of first odd integers =
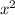
Three times of second odd integers =
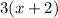
It is given that the sum of square of first odd integers and three times of second odd integers is 24. So, the required equation is:

Part c:
The equation is:

It can be written as:
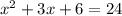
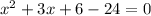
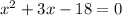
Splitting the middle term, we get

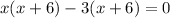
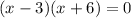
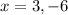
-6 is not an odd integer, so
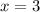 and the first odd integer is 3.
and the first odd integer is 3.
Second odd integer =
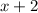
=
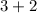
=

Therefore, the two consecutive odd integers are 3 and 5.