Question

Find two consecutive odd integers such that the square of the first added to 3 times the second, is 24. Part a: Define the variables. Part b: Set up an equations that can be solved to find the integers. Part c: Find the integers.

Answer 1

Given:

There are two consecutive odd integers such that the square of the first added to 3 times the second, is 24.

To find:

Part a: Define the variables.

Part b: Set up an equations that can be solved to find the integers.

Part c: Find the integers.

Solution:

Part a:

Let x be the first odd integers. Then next consecutive odd integer is
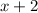`x+2`, because the difference between two consecutive odd integers is 2.

Part b:

Square of first odd integers =
`x^2`

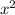
Three times of second odd integers =
`3(x+2)`

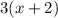
It is given that the sum of square of first odd integers and three times of second odd integers is 24. So, the required equation is:

`x^2+3(x+2)=24`

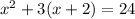
Part c:

The equation is:

`x^2+3(x+2)=24`

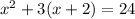
It can be written as:

`x^2+3x+6=24`

`x^2+3x+6-24=0`

`x^2+3x-18=0`

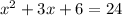
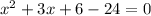
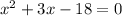
Splitting the middle term, we get

`x^2+6x-3x-18=0`

`x(x+6)-3(x+6)=0`

`(x-3)(x+6)=0`

`x=3,-6`

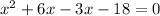
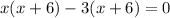
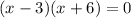
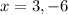
-6 is not an odd integer, so
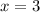`x=3` and the first odd integer is 3.

Second odd integer =
`x+2`

=
`3+2`

=
`5`

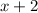
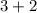
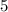
Therefore, the two consecutive odd integers are 3 and 5.