Answer:
The pair of points A and B to point C such that ∠ABC = 90° are;
1) A(-10, 5) and B(12, 16), C(18, 4)
2) A(12, -14) and B(-16, 21), C(-11, 25)
Explanation:
The angle formed between the points A and B to point C, ∠ABC is 90° when the the line passing through points A and B is perpendicular to the line passing through points B and C
Therefore, for ∠ABC = 90°
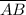 is perpendicular to
is perpendicular to
 (
(
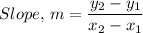
The slope of
 = -1/m, where, the slope of
= -1/m, where, the slope of
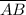 = m
= m
Each option is analyzed as follows;
1) A(3, 3) and B(12, 6) C(6, 52)
The slope of
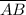 = (6 - 3)/(12 - 3) = 0.
= (6 - 3)/(12 - 3) = 0.

The slope of
 = (52 - 6)/(6 - 12) = -7.
= (52 - 6)/(6 - 12) = -7.
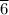 ≠ 1/(0.
≠ 1/(0.
 ) = 3
) = 3
∴
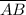 is not perpendicular to
is not perpendicular to
 and ∠ABC ≠ 90°
and ∠ABC ≠ 90°
2) A(-10, 5) and B(12, 16) C(16, -6)
The slope of
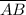 = (16 - 5)/(12 - (-10)) = 0.5
= (16 - 5)/(12 - (-10)) = 0.5
The slope of
 = (-6 - 16)/(16 - 12) = -5.5 ≠ 1/(0.5) = 2
= (-6 - 16)/(16 - 12) = -5.5 ≠ 1/(0.5) = 2
For point C(18, 4), we have;
The slope of
 = (4 - 16)/(18 - 12) = -2
= (4 - 16)/(18 - 12) = -2
∴ A(-10, 5) and B(12, 16) is perpendicular to C(18, 4)
∴ ∠ABC = 90°
3) A(-8, 3) and B(12, 8) C(18, 4)
The slope of
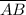 = (8 - 3)/(12 - (-8)) = 0.25
= (8 - 3)/(12 - (-8)) = 0.25
The slope of
 = (4 - 8)/(18 - 12) = -0.
= (4 - 8)/(18 - 12) = -0.
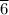 ≠ 1/(0.25) = 4
≠ 1/(0.25) = 4
∴
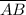 is not perpendicular to
is not perpendicular to
 and ∠ABC ≠ 90°
and ∠ABC ≠ 90°
4) A(12, -14) and B(-16, 21) C(-11, 25)
The slope of
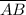 = (21 - (-14))/((-16) - 12) = -1.25
= (21 - (-14))/((-16) - 12) = -1.25
The slope of
 = (25 - (21))/((-11) - (-16)) = 0.8 = 1/(-1.25)
= (25 - (21))/((-11) - (-16)) = 0.8 = 1/(-1.25)
∴
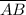 is perpendicular to
is perpendicular to
 and ∠ABC = 90°
and ∠ABC = 90°
5) A(-12, -19) and B(20, 45)
C(16, -6)
The slope of
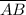 = (45 - (-19))/(20 - (-12)) = 2
= (45 - (-19))/(20 - (-12)) = 2
A(30, 20) and B(-20, -15)
The slope of
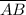 = (-15 - 30)/(-20 - 20) = 1.125
= (-15 - 30)/(-20 - 20) = 1.125
The slope of
 = (6 - 52)/(12 - 6) = -5.5 ≠ 1/(0.5) = 2
= (6 - 52)/(12 - 6) = -5.5 ≠ 1/(0.5) = 2
6) The slope of
 = (-6 - 16)/(16 - 12) = -5.5 ≠ 1/(0.5) = 2
= (-6 - 16)/(16 - 12) = -5.5 ≠ 1/(0.5) = 2
∴
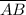 is not perpendicular to
is not perpendicular to
 and ∠ABC ≠ 90°
and ∠ABC ≠ 90°