Question

HELP! Find the value of sin 0 if tan 0 = 4; 180 < 0< 270

Answer 1

Hi there! Use the following identities below to help with your problem.

`\large \boxed{sin \theta = tan \theta cos \theta} \\ \large \boxed{tan^(2) \theta + 1 = {sec}^(2) \theta}`

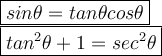
What we know is our tangent value. We are going to use the tan²θ+1 = sec²θ to find the value of cosθ. Substitute tanθ = 4 in the second identity.

`\large{ {4}^(2) + 1 = {sec}^(2) \theta } \\ \large{16 + 1 = {sec}^(2) \theta } \\ \large{ {sec}^(2) \theta = 17}`

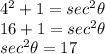
As we know, sec²θ = 1/cos²θ.

`\large \boxed{sec \theta = (1)/(cos \theta) } \\ \large \boxed{ {sec}^(2) \theta = \frac{1}{ {cos}^(2) \theta} }`

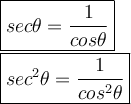
And thus,

`\large{ {cos}^(2) \theta = (1)/(17)} \\ \large{cos \theta = ( √(1) )/( √(17) ) } \\ \large{cos \theta = (1)/( √(17) ) \longrightarrow ( √(17) )/(17) }`

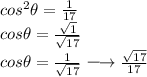
Since the given domain is 180° < θ < 360°. Thus, the cosθ < 0.

`\large{cos \theta = \cancel( √(17) )/(17) \longrightarrow cos \theta = - ( √(17) )/(17)}`

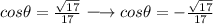
Then use the Identity of sinθ = tanθcosθ to find the sinθ.

`\large{sin \theta = 4 * ( - ( √(17) )/(17)) } \\ \large{sin \theta = - (4 √(17) )/(17) }`

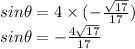
Answer

• sinθ = -4sqrt(17)/17 or A choice.