Hi there! Use the following identities below to help with your problem.
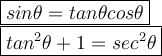
What we know is our tangent value. We are going to use the tan²θ+1 = sec²θ to find the value of cosθ. Substitute tanθ = 4 in the second identity.
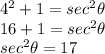
As we know, sec²θ = 1/cos²θ.
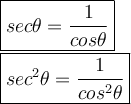
And thus,
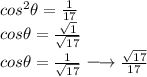
Since the given domain is 180° < θ < 360°. Thus, the cosθ < 0.
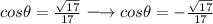
Then use the Identity of sinθ = tanθcosθ to find the sinθ.
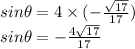
Answer
- sinθ = -4sqrt(17)/17 or A choice.