Question

A ballistic pendulum is a device for measuring bullet speeds. One of the simplest versions consists of a block of wood hanging from two long cords. (Two cords are used so that the bottom face of the block remains parallel to the floor as the block swings upward.) A 0.013-kg bullet traveling at 320 m/s hits a 3.0-kg ballistic pendulum. However, the block is not thick enough for this bullet, and the bullet passes through the block, exiting with one-third of its original speed.

Required:
How high above its original position does the block rise?

Answer 1

0.043 m upwards

Step-by-step explanation:

The mass of the bullet,
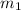`$m_1$` = 0.013 kg

Mass of the ballistic pendulum,
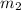`$m_2$` = 3 kg

Velocity of the bullet,
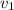`$v_1$` = 320 m/s

Therefore, from the law of conservation of momentum, we get

`$m_1v_1+m_2v_2=m_1v_1^1+m_2v_2^1$`

`$(0.013 * 320)+(3 * 0) = \left(0.013 * (320)/(0)\right) + (3 * v_2^1)$`

`$3 * v_2^1=2.774$`

`$v_2^1=0.92 \ m/s$`

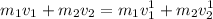
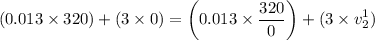
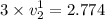
Therefore the required height to rise the block is given by :

`$(v_2^1)^2-v_2^2=2gh$`

`$h=((v_2^1)^2-v_2^2)/(2g)$`

`$h=((0.92)^2-0)/(2(-9.81))$`

`$h=-0.043 \ m$`

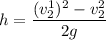
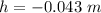
Therefore, the block moves upwards for 0.043 meters.