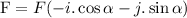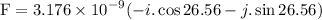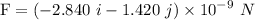Question

Determine the small gravitational force F which the copper sphere exerts on the steel sphere. Both spheres are homogeneous, and the value of r is 50 mm. Express your result as a vector.

Answer 1

We know that the volume of sphere is given by :

`$V=(4)/(3)\pi r ^3$`

Given r = 50 mm

The density of copper is :

`$\rho_c = 8910 \ kg/m^3$`

The density of steel is :

`$\rho_s = 7830\ kg/m^3$`

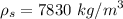
Therefore, mass of copper is :

`$m_c= V . \rho$`

`$m_c= (4)/(3) \pi (0.05)^3 * 8910$`

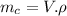
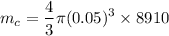
= 4.665 kg

= 4665 g

Similarly, mass of steel is :

`$m_s= V . \rho$`

`$m_s= (4)/(3) \pi (0.025)^3 * 7830$`

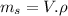
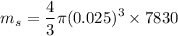
= 0.512 kg

= 512 g

Now the distance between the centers of the particles is by Pythagoras theorem,

`$l^2=(4r)^2+(2r)^2$`

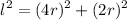
l = 4.472 x r

= 4.472 x 50

= 224 mm

= 0.224 m

From the law of gravitation,

We know,
`G = 6673 * 10^(-11) \ m^3 / kg-s^2`

∴
`$F=G* (m_c * m_s)/(l^2)$`

`$F=6.673 * 10^(-11)* (4.665 * 0.512)/((0.224)^2)$`

`$F = 3.176 * 10^(-9) \ N$`

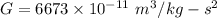
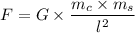
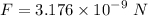
Now,

`$\alpha = \tan^(-1) \left( (2r)/(4r)\right)$`

=
`$26.56^\circ$`

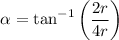
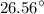
Therefore, we can write it in the vector form as

`$\text{F}=F(-i . \cos \alpha - j. \sin \alpha)$`

`$\text{F}=3.176 * 10^(-9)(-i . \cos 26.56 - j. \sin 26.56)$`

`$\text{F}=(-2.840\ i- 1.420 \ j) * 10^(-9) \ N$`