Question

Can someone help i don't get this problem

Answer 1

Answer:
`√(3)+√(5)`

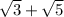
On a keyboard, we could type this as sqrt(3) + sqrt(5)

==============================================================

Step-by-step explanation:

The given expression is considered a nested radical because one radical, the
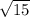`√(15)`, is buried inside another radical.

Let's assume that nested radical is of the form
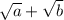`√(a)+√(b)` where a & b are positive real numbers.

Set the given expression equal to
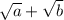`√(a)+√(b)` and square both sides to see what happens. We'll do a bit of algebra to simplify and rearrange things a bit as well. See the steps below.

`\sqrt{8+2√(15)} = √(a)+√(b)\\\\\left(\sqrt{8+2√(15)}\right)^2 = \left(√(a)+√(b)\right)^2\\\\8+2√(15) = \left(√(a)\right)^2 + 2√(a)√(b) + \left(√(b)\right)^2\\\\8+2√(15) = a + 2√(ab) + b\\\\8+2√(15) = (a+b) + 2√(ab)\\\\`

If we equate terms, we get this system of equations

`\begin{cases}8 = a+b\\2√(15) = 2√(ab)\\\end{cases}`

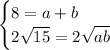
Solve the first equation for 'a' to get a = 8-b

------------------------------

Let's plug a = 8-b into the second equation and solve for 'b'

`2√(15) = 2√(ab)\\\\√(15) = √(ab)\\\\15 = ab\\\\15 = (8-b)b \ \ \text{ .... replace a with 8-b}\\\\15 = 8b-b^2\\\\b^2-8b+15 = 0\\\\(b-3)(b-5) = 0\\\\b-3 = 0 \ \text{ or } \ b-5 = 0\\\\b = 3 \ \text{ or } \ b = 5\\\\`

If b = 3, then a = 8-b = 8-3 = 5

If b = 5, then a = 8-b = 8-5 = 3

We have this symmetry going on with 'a' and b. If one value is 3, then the other is 5, and vice versa. The order doesn't matter.

That means the equation

`\sqrt{8+2√(15)} = √(a)+√(b)\\\\`

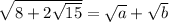
updates to

`\sqrt{8+2√(15)} = √(3)+√(5)\\\\`

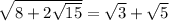
The order doesn't matter on the right side since we can add two numbers in any order.

---------

You can use your calculator to confirm the answer.

Note that

`\sqrt{8+2√(15)} \approx 3.968118785`

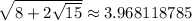
and

`√(3)+√(5) \approx 3.968118785`

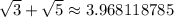
both result in the same decimal approximation to help show the two sides are equal.

Answer 2

the answer is 10•57(approximated as 10•6)