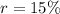Answer:
(a) The population in 2000 is 450
(b) 15% decreases each year
Explanation:
Given
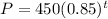 --- since 2000
--- since 2000
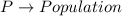
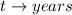
Solving (a): The population in 2000
First calculate t
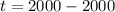 --- years since 200
--- years since 200
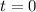
So, we have:
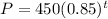
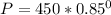
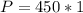
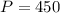
Solving (b): Rate of population decrease
A function that decreases is represented as:
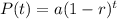
Where
 rate of decrement
rate of decrement
Compare
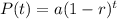 and
and
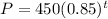
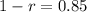
Collect like terms

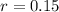
Express as percentage