Question

Find the 64th term of the arithmetic sequence

−
4
,
−
21
,
−
38
,
.
.
.
−4,−21,−38,...

Answer 1

The 64th term of the arithmetic sequence is -1075.

Explanation:

Arithmetic sequence:

In an arithmetic sequence, the difference between consecutive terms, called common difference, is always the same.

The nth term of an arithmetic sequence is given by:

`a_n = a_1 + (n-1)d`

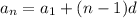
In which
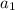`a_1` is the first term.

−4,−21,−38

First term -4, so
`a_1 = -4`

Common difference of
`d = -38 - (-21) = -21 - (-4) = -17`

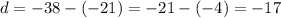
Thus

`a_n = a_1 + (n-1)d`

`a_n = -4 - 17(n-1)`

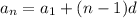
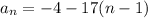
Find the 64th term of the arithmetic sequence

This is
`a_(64)`. So

`a_n = -4 - 17(n-1)`

`a_(64) = -4 - 17(64-1) = -4 - 1071 = -1075`

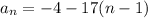
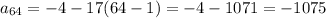
The 64th term of the arithmetic sequence is -1075.