Question

Your class is selling boxes of flower seeds as a fundraiser. The total profit p depends on the amount x that your class charges for each box of seeds. The equation p= -0.5x2 + 36x - 231 models the profit of the fundraiser. What's the smallest amount, in dollars, that you can charge and make a profit of at least $363?​

Answer 1

The least amount is $75.50

Explanation:

Given

`p \to profit`

`x \to amount`

`p = -0.5x^2 + 36x - 231`

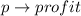
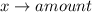
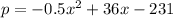
Required

The smallest amount to make at least 363

We have:

`p = -0.5x^2 + 36x - 231`

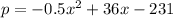
Rewrite as:

`-0.5x^2 + 36x - 231=p`

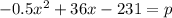
Substitute 363 for p

`-0.5x^2 + 36x - 231 = 363`

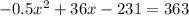
Collect like terms

`-0.5x^2 + 36x - 231 + 363 = 0`

`-0.5x^2 + 36x + 132 = 0`

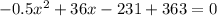
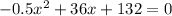
Using quadratic formula, we have:

`x = (-b \± √(b^2 - 4ac))/(2a)`

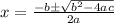
Where:

`a = -0.5; b= 36; c = 132`

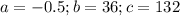
So, we have:

`x = (-36 \± √(36^2 - 4*-0.5*132))/(2*-0.5)`

`x = (-36 \± √(1560))/(-1)`

`x = (-36 \± 39.50)/(-1)`

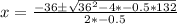
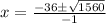
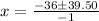
Split

`x = (-36 + 39.50)/(-1); x = (-36 - 39.50)/(-1)`

`x = (3.50)/(-1); x = (-75.50)/(-1)`

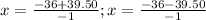
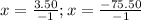
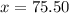`x = 75.50` and
`x = -3.50`

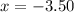
The amount can't be negative.

So:

`x = 75.50`

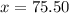
Hence, the least amount is $75.50