Answer:
Area: 16
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Calculus
Derivatives
Derivative Notation
Integrals - Area under the curve
Trig Integration
Integration Rule [Fundamental Theorem of Calculus 1]:
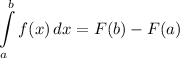
Integration Property [Multiplied Constant]:
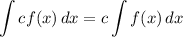
Integration Property [Addition/Subtraction]:
![\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/r5yh324r81plt97j3zrr5qi2xxczxlqi34.png)
U-Substitution
Explanation:
Step 1: Define
Identify
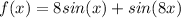
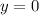
Bounds of Integration: 0 ≤ x ≤ π
Step 2: Find Area Pt. 1
- Set up integral:
![\displaystyle A = \int\limits^(\pi)_0 {[8sin(x) + sin(8x)]} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/yp9dmujamgdtzo25rjde9wn6z28xy8fh71.png)
- Rewrite integral [Integration Property - Addition/Subtraction]:
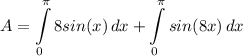
- [1st Integral] Rewrite [Integration Property - Multiplied Constant]:
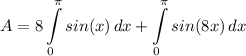
- [1st Integral] Integrate [Trig Integration]:
![\displaystyle A = 8[-cos(x)] \bigg| \limits^(\pi)_0 + \int\limits^(\pi)_0 {sin(8x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/hnytdj6z5i3ni8guxhnmhothozta80x2u5.png)
- [1st Integral] Evaluate [Integration Rule - FTC 1]:
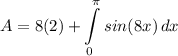
- Multiply:
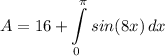
Step 3: Identify Variables
Identify variables for u-substitution.
u = 8x
du = 8dx
Step 4: Find Area Pt. 2
- [Integral] Rewrite [Integration Property - Multiplied Constant]:
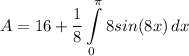
- [Integral] U-Substitution:
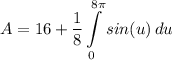
- [Integral] Integrate [Trig Integration]:
![\displaystyle A = 16 + (1)/(8)[-cos(u)] \bigg| \limits^(8\pi)_0](https://img.qammunity.org/2022/formulas/mathematics/high-school/7vhzpvkt9oad4i1imvyb62iod3nmwf59bz.png)
- [Integral] Evaluate [Integration Rule - FTC 1]:
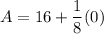
- Simplify:
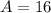
Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Integration - Area under the curve
Book: College Calculus 10e