Question

Consider the following functions. (See attachment)
Find the area of the region.

Answer 1

Area:
`\displaystyle (1)/(2)`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Functions
• Function Notation
• Graphing Functions
• Exponential Rule [Root Rewrite]:
  `\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`

Calculus

Derivatives

Derivative Notation

Derivative of a constant is 0

Area - Integrals

• Area under a curve
• Area between 2 curves

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

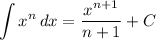
Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

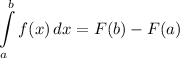
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

U-Substitution

Area of a Region Formula:
`\displaystyle A = \int\limits^b_a {[f(x) - g(x)]} \, dx`

Explanation:

Step 1: Define

Identify functions

`\displaystyle f(x) = \sqrt[3]{x - 9}`

`\displaystyle g(x) = x - 9`

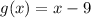
Step 2: Identify Info

Graph the functions - See Attachment

[1st Integral] Bounds: [8, 9], g(x) top function/f(x) bottom function

[2nd Integral] Bounds: [9, 10], f(x) top function/g(x) bottom function

Step 3: Find Area Pt. 1

1. Set up integrals [Area of a Region Formula]:
   `\displaystyle A = \int\limits^9_8 {[(x - 9) - \sqrt[3]{x - 9}]} \, dx + \int\limits^(10)_9 {[\sqrt[3]{x - 9} - (x - 9)]} \, dx`
2. Rewrite integrals [Integration Property - Addition/Subtraction]:
   `\displaystyle A = \int\limits^9_8 {(x - 9)} \, dx - \int\limits^9_8 {\sqrt[3]{x - 9}} \, dx + \int\limits^(10)_9 {\sqrt[3]{x - 9}} \, dx - \int\limits^(10)_9 {(x - 9)} \, dx`
3. Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle A = (x^2 - 9x) \bigg| \limits^9_8 - \int\limits^9_8 {\sqrt[3]{x - 9}} \, dx + \int\limits^(10)_9 {\sqrt[3]{x - 9}} \, dx - (x^2 - 9x) \bigg| \limits^9_8`
4. Evaluate [Integration Rule - FTC 1]:
   `\displaystyle A = (-1)/(2) - \int\limits^9_8 {\sqrt[3]{x - 9}} \, dx + \int\limits^(10)_9 {\sqrt[3]{x - 9}} \, dx - (1)/(2)`
5. Subtract:
   `\displaystyle A = -\int\limits^9_8 {\sqrt[3]{x - 9}} \, dx + \int\limits^(10)_9 {\sqrt[3]{x - 9}} \, dx - 1`
6. Rewrite [Exponential Rule - Root Rewrite]:
   `\displaystyle A = -\int\limits^9_8 {(x - 9)^{(1)/(3)}} \, dx + \int\limits^(10)_9 {(x - 9)^{(1)/(3)}} \, dx - 1`

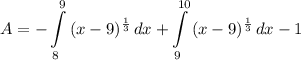
Step 4: Identify Variables

Identify variables for u-substitution.

u = x - 9

du = dx

Step 5: Find Area Pt. 2

1. [Integrals] U-Substitution:
   `\displaystyle A = -\int\limits^0_(-1) {u^{(1)/(3)}} \, du + \int\limits^1_0 {u^{(1)/(3)}} \, du - 1`
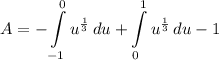
2. [Integrals] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle A = -((3)/(4)u^{(4)/(3)}) \bigg| \limits^0_(-1) + ((3)/(4)u^{(4)/(3)}) \bigg| \limits^1_0 - 1`
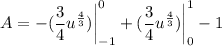
3. Evaluate [Integration Rule - FTC 1]:
   `\displaystyle A = -((-3)/(4)) + (3)/(4) - 1`
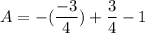
4. Simplify:
   `\displaystyle A = (1)/(2)`

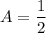
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Integrals - Area between 2 curves

Book: College Calculus 10e