Answer:
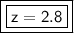
Explanation:
The z-score helps describe a value's relationship to the mean. It tells us how many standard deviations a value is from the mean. The formula is:
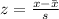
where x is the value, x-bar is the mean, and s is the standard deviation.
We know the data set has a mean of 25 and a standard deviation of 5. The value we are finding the z score for is 39.
Substitute the values into the formula.
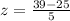
Solve the numerator.
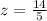
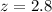
The z-score for 39 is 2.8. This means a value of 39 is 2.8 standard deviations greater than the mean.