N manufacturing a product, 85% of the units that are produced are not defective. Of the products inspected, 10% of the good ones (i.e., not defective) are falsely seen as defect…

Question

asked Mar 10, 2022 193k views

1 Answer

The Real Napster · Answer 1 · 2022-03-16T11:05:50+0000

Answer:

0.0097 = 0.97% probability that it is defective

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

$P(B|A) = (P(A \cap B))/(P(A))$

In which

P(B|A) is the probability of event B happening, given that A happened.

$P(A \cap B)$ is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Product is shipped.

Event B: It is defective.

Probability of the product being shipped:

100 - 10 = 90% of 85%(not defective).

5% of 100 - 85 = 15%(defective). So

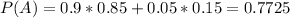
P(A) = 0.9*0.85 + 0.05*0.15 = 0.7725

Probability of being shipped and being defective:

5% of 15%. So

$P(A \cap B) = 0.05*0.15 = 0.0075$

What is the probability that it is defective?

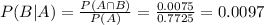
$P(B|A) = (P(A \cap B))/(P(A)) = (0.0075)/(0.7725) = 0.0097$

0.0097 = 0.97% probability that it is defective