Question

Solve the quadratic equation below

(3x+9)(x−4)=0

Answer 1

x = 4

x = - 3

Explanation:

Method 1

Quadratic Formula

(3x + 9)(x - 4) = 0

3x(x - 4) + 9(x - 4) = 0

3x² - 12x + 9(x - 4) = 0

3x² - 12x + 9x - 36 = 0

3x² - 3x - 36 = 0

3(x² - x - 12) = 0

`(3(x^(2) - x - 12))/(3) = (0)/(3)`

`x={\frac{-b±\sqrt{b^(2)-4ac } }{2a} }`

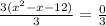
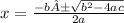
Ignore the A after the -b, wouldn't let me type it correctly. Ignore the A for the rest of the explanation as well.

x² - x - 12 = 0

a = 1

b = - 1

c = - 12

`x={\frac{-(-1)±\sqrt{(-1)^(2)-4(1(-12)) } }{2(1)} }`

`x={(-(-1)±√(1-4(1(-12)) ) )/(2(1)) }`

`x={(-(-1)±√(1+48 ) )/(2(1)) }`

`x={(-(-1)±√(49 ) )/(2(1)) }`

`x={(1±7 )/(2(1)) }`

`x={(1±7 )/(2) }`

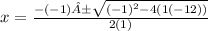
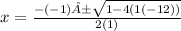
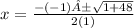
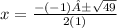
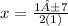
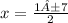
Separate into two equations.

One with addition and the other with subtraction.

`x={(1+7 )/(2) }`

`x={(1-7 )/(2) }`

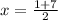
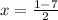
x = 4

x = - 3

Method 2

Factors

(3x + 9)(x - 4) = 0

3x(x - 4) + 9(x - 4) = 0

3x² - 12x + 9(x - 4) = 0

3x² - 12x + 9x - 36 = 0

3x² - 3x - 36 = 0

3(x² - x - 12) = 0

3(x² + 3x - 4x - 12) = 0

3(x² + 3x + (- 4x - 12)) = 0

3(x(x + 3) - 4(x + 3)) = 0

3(x - 4)(x + 3) = 0

Create separate equations

x - 4 = 0

x + 3 = 0

x - 4 = 0 ⇒ x - 4 + 4 = 0 + 4 ⇒ x = 4

x + 3 = 0 ⇒ x + 3 - 3 = 0 - 3 ⇒ x = - 3

x = 4

x = - 3

Answer 2

x = {-3, 4}

Explanation:

(3x + 9)(x − 4) = 0

Solution 1

3x + 9 = 0

3x = -9

x = -3

Solution 2

x - 4 = 0

x = 4

x = {-3, 4}

---------------------------

if by solve you meant expand

(3x + 9)(x − 4) = 0

3x² - 12x + 9x - 36 = 0

3x² - 3x - 36 = 0