Question

Prove these identities
(i) secx cosecx - cotx = tanx
​

Answer 1

`(A)\frac 1 {cosx} \frac 1 {sin x} - \frac {cosx} {sin x} = \frac {sin x} {cosx} \\\\(B)(1-cos^2 x )/(cos x sin x) = \frac {sin x} {cosx} \\\\(C) ((sin^2x + cos^2x)-cos^2 x )/(cos x sin x) = \frac {sin x} {cosx} \\\\(D) (sin^2x )/(cos x sin x) = \frac {sin x} {cosx}\\\\(E)\frac {sin x}{cos x} = \frac {sin x}{cos x}`

In step A, you replace all trigonometric functions with their definitions in terms of sine and cosine.

In step B, you add the two together as you add fractions.

In step C, you replace 1 with the sum of the squares of sine and cosine.
In step D, you add the cosine terms together so they disappear.

In step E, finally, you divide numerator and denominator by
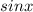`sin x`.