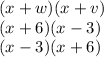Answer:
C.
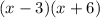
Explanation:
I think the equation meant
 ?
?
Anyways, to factor these kinds of quadratic, keep into consideration:
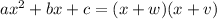
ONLY if:
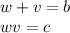
Start off by finding factors of c, which in this case, -18:
±(1, 2, 3, 6, 9, 18)
If one of the numbers is negative then the other number must be positive.
Find which two factors will sum up to b, which in this case, is 3.
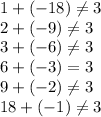
The only two factors that work are 6 and -3.
Replace them into the factored form: