Question

5) In the figure, triangle ABC is a right triangle at B. If CD = 15, find BC to the nearest tenth.

Answer 1

BC ≈ 4.0

Explanation:

∠ DCA = 180° - 70° = 110° ( adjacent angles )

∠ DAC = 180° - (30 + 110)° ← sum of angles in triangle

∠ DAC = 180° - 140° = 40°

Using the Sine rule in Δ ACD to find common side AC

`(AC)/(sin30)` =
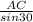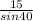`(15)/(sin40)` ( cross- multiply )

AC × sin40° = 15 × sin30° ( divide both sides by sin40° )

AC =
`(15sin30)/(sin40)` ≈ 11.668

Using the cosine ratio in right triangle ABC

cos70° =
`(adjacent)/(hypotenuse)` =
`(BC)/(AC)` =
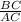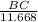`(BC)/(11.668)` ( multiply both sides by 11.668 )

11.668 × cos70° = BC , then

BC ≈ 4.0 ( to the nearest tenth )