Question

You want to decaffeinate your coffee by extracting the caffeine outwith dichloromethane. It's too late to extract the caffeinefrom the coffee beans because you've already brewed yourself a 200mL cup of coffee. Your particular brand of coffee contains100 mg of caffeine in that 200mL cup. The partitioncoefficient of caffeine in dichloromethane/water is 9.0.

How much caffeine would still be in your 200 mL if you did:
A. One extraction using 200 mL o fdichloro methane
B. Two extractions using 100 mL of dichloro methane each.

Answer 1

The partition coefficient

`$k_d= \frac{\text{(mass of caffeine in }CH_2Cl_2 / \text{volume of }CH_2Cl_2)}{\text{(mass of caffeine in water/ volume of water)}}$`

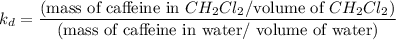
= 9.0

A). 1 x 200 mL extraction

Let m be the mass of caffeine in water

Mass of caffeine in
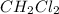`$CH_2Cl_2$` = 100 - m

∴
`$((100-m)/200)/(m/200)=9$`

`$(100-m)/(m)=9$`

`$10 \ m = 100$`

`$m=(100)/(10)$`

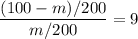
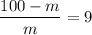
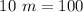
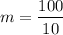
= 10

Therefore, the mass remaining in the coffee is m = 10 mg

B). 2 x 100 mL extraction

First extraction :

Let
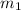`$m_1$` be the mass of the caffeine in water.

Mass of caffeine in
`$CH_2Cl_2$` = 100 - m

∴
`$((100-m_1)/100)/(m_1/200)=9$`

`$(100-m_1)/(m_1)=9$`

`$5.5 \ m_1 = 100$`

`$m_1=(100)/(5.5)$`

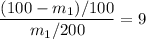
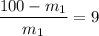
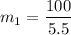
= 18.18

Mass remaining in the coffee after the 1st extraction
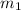`$m_1$` = 18.18 mg

Second extraction:

Let
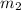`$m_2$` be the mass of the caffeine in water.

Mass of caffeine in
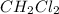`$CH_2Cl_2$` = 18.18 -
`$m_2$`

∴
`$((18.18-m_2)/100)/(m_2/200)=9$`

`$(18.18-m_2)/(m_2)=9$`

`$5.5 \ m_2 = 18.18$`

`$m_1=(18.18)/(5.5)$`

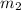
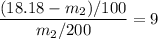
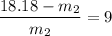
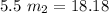
= 3.3

Mass remaining in the coffee after the 1st extraction
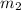`$m_2$` = 3.3 mg