Question

F(x)= square root of x-5. find f-1 (x) and it’s domain

Answer 1

B. f ^ -1 (x) = (x + 5) ^ 2;

x > -5

Explanation:

Ap e x

Answer 2

Option B.

Explanation:

Inverse function:

Suppose we have a function y = f(x). To find the inverse function, we exchange x and y on the original function, and then isolate y.

The domain of the inverse function(x values) is the range of the original function(y values).

Original function:

`f(x) = √(x) - 5`

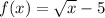
Domain is
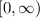`[0,\infty)`, and when
`x = 0, f(x) = -5`. So the range is
`[-5,\infty]`, that is,
`y \geq -5`

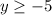
Inverse function:

`y = √(x) - 5`

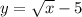
Exchanging x and y

`x = √(y) - 5`

`√(y) = x + 5`

`(√(y))^2 = (x+5)^2`

`y = (x+5)^2`

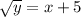
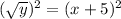
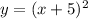
The inverse function is
`f^(-1)(x) = (x+5)^2`

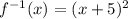
Domain:

Range of the original function is
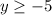`y \geq -5`, so the domain of the inverse function is
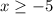`x \geq -5`. The correct answer is given by option B.