Answer:
Option B.
Explanation:
Inverse function:
Suppose we have a function y = f(x). To find the inverse function, we exchange x and y on the original function, and then isolate y.
The domain of the inverse function(x values) is the range of the original function(y values).
Original function:
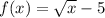
Domain is
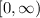 , and when
, and when
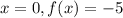 . So the range is
. So the range is
![[-5,\infty]](https://img.qammunity.org/2022/formulas/mathematics/college/hydhbuw8i02pwdh3sexedponezvkj93sda.png) , that is,
, that is,
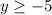
Inverse function:
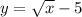
Exchanging x and y
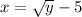
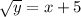
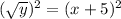
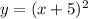
The inverse function is
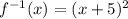
Domain:
Range of the original function is
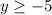 , so the domain of the inverse function is
, so the domain of the inverse function is
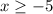 . The correct answer is given by option B.
. The correct answer is given by option B.