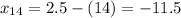Answer:
The common difference is -1.
The last term (the 14th term) is -11.5.
Explanation:
In an arithmetic sequence, the second term is 0.5 and the sum of the first 14 terms is -70.
We want to determine the: (a) common difference and (b) the last term.
We can write an explicit formula to represent the sequence. An arithmetic sequence can be modeled by the formula:

Where a is the initial term, d is the common difference, and n represents the nth term.
Since the second term is 0.5:
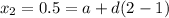
Simplify:
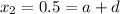
The sum of an arithmetic sequence is given by the formula:
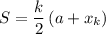
Where k is the number of terms and x_k is the last term.
Since the sum of the first 14 terms is -70, S = -70 and k = 14:
Using our explicit formula, the last term is:

Substitute:
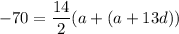
Simplifiy:
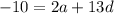
Rewrite the equation for the second term:
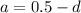
Substitute:
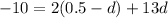
Simplify:
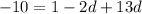
Solve for d:
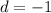
Hence, our common difference is -1.
Solve for a, the initial term:
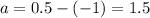
So, our explicit formula is now:
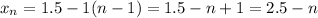
So, the last term (which is 14) is: