Question

One diagonal of a rhombus is four times the length of the other diagonal. The area of the rhombus is 98 square feet. Identify an equation that can be used to find the length of each diagonal. Let x represent the length of the shorter diagonal. Then find the length of each diagonal. Round decimal answers to the nearest tenth.

Answer 1

shorter length = 7 feet

longer length = 28 feet

Equation : 98 = 2x²

Explanation:

A rhombus is a four sides quadrilateral with the four sides equal in length

The area of a rhombus =
`(1)/(2)pq`

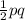
where p and q are the two diagonals

shorter length = x

longer length = 4x

98 = (1/2) ×4x × x

98 = 4x² x (1/2)

98 = 2x²

divide both sides of the equation by 2

49 = x²

find the square root of both sides

x = 7 ft

longer sides = 4 x 7 = 28 ft