Answer:
shorter length = 7 feet
longer length = 28 feet
Equation : 98 = 2x²
Explanation:
A rhombus is a four sides quadrilateral with the four sides equal in length
The area of a rhombus =
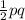
where p and q are the two diagonals
shorter length = x
longer length = 4x
98 = (1/2) ×4x × x
98 = 4x² x (1/2)
98 = 2x²
divide both sides of the equation by 2
49 = x²
find the square root of both sides
x = 7 ft
longer sides = 4 x 7 = 28 ft