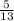Answer:
Solution given;
Sec θ=-
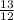
cotθ< 0,
It lies in second quadrant.
where sin and cosec is positive.
Now
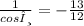
cosθ=

 =
=

b=12
h=13
By using Pythagoras law
p=
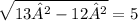
Now
exact values of tan θ=
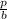 =
=
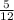
since it lies in II quadrant
tan θ=-
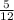
and
sinθ=
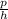 =
=
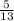
since it lies in II quadrant
sin θ=