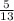Question

Let 0 be an angle such that sec0= -13/12 and cot0<0. Find the exact values of tan0 and sin0.

Answer 1

tan 0 = -2.4

sin 0 = 0.42

Explanation:

sec 0 = -13/12 => cos 0 = -12/13

cot 0 < 0 => tan 0 < 0

so, the angle is on second quadrant

=> tan 0 = -12/5 = -2.4

=> sin 0 = 5/12 = 0.42

Answer 2

Solution given;

Sec θ=-
`(13)/(12)`

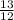
cotθ< 0,

It lies in second quadrant.

where sin and cosec is positive.

Now

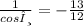
`(1)/(cosθ)=-(13)/(12)`

cosθ=
`(12)/(13)`

`(b)/(h)`=
`(12)/(13)`

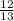
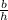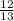
b=12

h=13

By using Pythagoras law

p=
`√(13²-12²)=5`

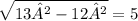
Now

exact values of tan θ=
`(p)/(b)`=
`(5)/(12)`

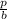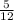
since it lies in II quadrant

tan θ=-
`(5)/(12)`

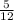
and

sinθ=
`(p)/(h)`=
`(5)/(13)`

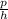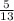
since it lies in II quadrant

sin θ=
`(5)/(13)`