Answer:
Center: (0, 0); Vertices: (0, -5), (0, 5); Foci: (0, -4), (0, 4)
Explanation:
So we're asked to find the center, vertices, and foci of the ellipse with the equation

Original Formula:
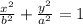
So a = 5 and b = 3 and the major axis is vertical.
Center: (0, 0)
Major Axis = 2a
Minor Axis = 2b
Distance between Foci = 2c
So that means:
Major Axis = (-3, 0); (3, 0)
Minor Axis = (0, -5); (0, 5)

Focus = (0, -4); (0, 4)
So in conclusion:
Center: (0, 0); Vertices: (0, -5), (0, 5); Foci: (0, -4), (0, 4)