Question

Find the center, vertices, and foci of the ellipse with equation x squared divided by 9 plus y squared divided by 25

Answer 1

Center: (0, 0); Vertices: (0, -5), (0, 5); Foci: (0, -4), (0, 4)

Explanation:

So we're asked to find the center, vertices, and foci of the ellipse with the equation
`(x^(2) )/(9)+(y^(2) )/(25)=1`

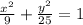
Original Formula:
`(x^(2) )/(b^(2) )+(y^(2) )/(a^(2) )=1`

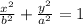
So a = 5 and b = 3 and the major axis is vertical.

Center: (0, 0)

Major Axis = 2a

Minor Axis = 2b

Distance between Foci = 2c

So that means:

Major Axis = (-3, 0); (3, 0)

Minor Axis = (0, -5); (0, 5)

`c^(2) = a^(2) - b^(2) \\c^(2) = 5^(2) -3^(2) \\c^(2) = 25 -9 \\c^(2)=16\\c=4`

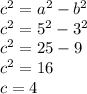
Focus = (0, -4); (0, 4)

So in conclusion:

Center: (0, 0); Vertices: (0, -5), (0, 5); Foci: (0, -4), (0, 4)

Answer 2

`C=(0,0)`

`F=(\pm 4,0)`

`V=(\pm 5,0)`

Step-by-step explanation:

From the question we are told that:

The Equation

`(x^2)/(9)*(y^2)/(25)`

Generally

From the Equation

`a^2=25`

`a=5\\b^2=9\\b=3`

Therefore

`c=√(a^2-b^2)`

`c=√(25-9)`

`c=√(16)`

`c=4`

Generally the equation for center is mathematically given by

`C=(h,k)`

`C=(0,0)`

Generally the equation for foci is mathematically given by

`F=(h,k \pm c,0)`

`F=(\pm 4,0)`

Generally the equation for vertice is mathematically given by

`V=(h,k \pm a,0)`

`V=(\pm 5,0)`