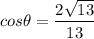Question

Find the value of the trig function indicated.

Answer 1

`\displaystyle cos\theta = (2√(13))/(13)`

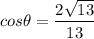
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Trigonometry

[Right Triangles Only] Pythagorean Theorem: a² + b² = c²

• a is a leg
• b is another leg
• c is the hypotenuse

[Right Triangles Only] SOHCAHTOA

[Right Triangles Only] cosθ = adjacent over hypotenuse

Explanation:

Step 1: Define

Identify variables

a = 8

b = 12

c

Step 2: Solve for c

1. Substitute in variables [Pythagorean Theorem]: 8² + 12² = c²
2. Evaluate exponents: 64 + 144 = c²
3. Add: 208 = c²
4. [Equality Property] Square root both sides: √208 = c
5. Rewrite: c = √208
6. Simplify: c = 4√13

Step 3: Define Pt. 2

Identify variables

Angle θ

Adjacent leg = 8

Hypotenuse = 4√13

Step 4: Find

1. Substitute in variables [Cosine]:
   `\displaystyle cos\theta = (8)/(4√(13))`
2. Rationalize:
   `\displaystyle cos\theta = (2√(13))/(13)`

Answer 2

Solution given;

In right angled triangle with respect to θ

perpendicular: opposite side: [P]=12

base:adjacent:[b]=8

hypotenuse [h]=?

cosθ=?

According to the Pythagoras law

h²=p²+b²

h²=12²+8²

h=
`√(208)`

h=
`4√(13)`

Now

we have

Cos θ=
`(adjacent)/(hypotenuse)`

Cos θ=
`(8)/(4√(13))`

by rationalising it

Cos θ=
`(2√(13))/(√(13)×√(13))`

Cos θ=
`(2√(13))/(13)`

is a required answer.