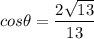Answer:
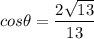
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Equality Properties
- Multiplication Property of Equality
- Division Property of Equality
- Addition Property of Equality
- Subtraction Property of Equality
Trigonometry
[Right Triangles Only] Pythagorean Theorem: a² + b² = c²
- a is a leg
- b is another leg
- c is the hypotenuse
[Right Triangles Only] SOHCAHTOA
[Right Triangles Only] cosθ = adjacent over hypotenuse
Explanation:
Step 1: Define
Identify variables
a = 8
b = 12
c
Step 2: Solve for c
- Substitute in variables [Pythagorean Theorem]: 8² + 12² = c²
- Evaluate exponents: 64 + 144 = c²
- Add: 208 = c²
- [Equality Property] Square root both sides: √208 = c
- Rewrite: c = √208
- Simplify: c = 4√13
Step 3: Define Pt. 2
Identify variables
Angle θ
Adjacent leg = 8
Hypotenuse = 4√13
Step 4: Find
- Substitute in variables [Cosine]:
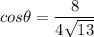
- Rationalize: