Hi there! You still remember the Pythagorean Theorem, right? It's useful when it comes to finding a missing leg or side of a right triangle. If you forget then here it is:
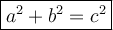
Define c = hypotenuse while a and b can be both adjacent and opposite (because a²+b²=b²+a² via addition property)
Since we are missing the adjacent side. Thus,
We define a = 6 and c = 14.
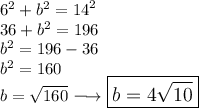
Put the value of b in a calculator then round to the nearest tenth and get 12.6
Thus, the value of b ≈ 12.6
Next we are going to find the angle in degree. We now know that b ≈ 12.6 or 4sqrt(10)
We can find the value of angle A by using tan or sin but I will use sin instead. Recall the sine ratio which is opposite to hypotenuse. Thus,
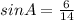
Use arcsin(6/14) and put it in calculator.
Then put the decimal value of arcsin in sin and convert in degree form which we should get 24. 555°. Round to the nearest whole number and we get 25°
Thus, the angle A is 25°
Next is we are finding the value of angle B. We aren't going to use any formula or equation. Recall that three angles add up to 180°.
Thus, 25° + 90° + x = 180°
90° comes from a right angle.
115+x = 180
x = 180-115
x = 65°
Thus, the angle B is 65°
Answer
- b ≈ 12.6 or 4sqrt(10)
- angle A = 25°
- angle B = 65°