Question

Solve the right triangle. See image below.

Answer 1

Hi there! You still remember the Pythagorean Theorem, right? It's useful when it comes to finding a missing leg or side of a right triangle. If you forget then here it is:

`\large \boxed{ {a}^(2) + {b}^(2) = {c}^(2) }`

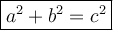
Define c = hypotenuse while a and b can be both adjacent and opposite (because a²+b²=b²+a² via addition property)

Since we are missing the adjacent side. Thus,

We define a = 6 and c = 14.

`\large{ {6}^(2) + {b}^(2) = {14}^(2) } \\ \large{36 + {b}^(2) = 196} \\ \large{ {b}^(2) = 196 - 36} \\ \large{ {b}^(2) = 160} \\ \large{ b = √(160) \longrightarrow \boxed{b = 4 √(10) }}`

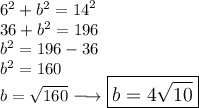
Put the value of b in a calculator then round to the nearest tenth and get 12.6

Thus, the value of b ≈ 12.6

Next we are going to find the angle in degree. We now know that b ≈ 12.6 or 4sqrt(10)

We can find the value of angle A by using tan or sin but I will use sin instead. Recall the sine ratio which is opposite to hypotenuse. Thus,

`\large{sinA = (6)/(14) }`

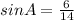
Use arcsin(6/14) and put it in calculator.

Then put the decimal value of arcsin in sin and convert in degree form which we should get 24. 555°. Round to the nearest whole number and we get 25°

Thus, the angle A is 25°

Next is we are finding the value of angle B. We aren't going to use any formula or equation. Recall that three angles add up to 180°.

Thus, 25° + 90° + x = 180°

90° comes from a right angle.

115+x = 180

x = 180-115

x = 65°

Thus, the angle B is 65°

Answer

• b ≈ 12.6 or 4sqrt(10)
• angle A = 25°
• angle B = 65°