Question

How to solve it?


`\int\limits^a_b {x^2+2x} \, dx`

Answer 1

Hi there! Assume that this is your question.

`\large{ \int \limits^a_b ( {x}^(2) + 2x)dx}`

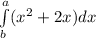
Before we get to Integral, you have to know Differentiation first. If you know how to differentiate a polynomial function then we are good to go in Integral!

We call the function that we are going to integrate as Integrand. Integrand is a function that's differentiated. In Integral, Integrating requires you to turn the function from differentiated to an original function.

For Ex. If the Integrand is x² then the original function is (1/3)x³ because when we differentiate (1/3)x³, we get x²

`\large{f(x) = (1)/(3) {x}^(3) \longrightarrow f'(x) = {x}^(2) } \\ \large{f'(x) = 3( (1)/(3) ) {x}^(3 - 1) } \\ \large{f'(x) = {x}^(2) }`

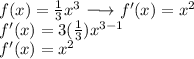
So when we Integrate, make sure to convert Integrand as in original function. From the question, our Integrand is x²+2x. The function is in differentiated form. We know that x² is from (1/3)x³ and 2x comes from x²

`\large{ f(x) = {x}^(2) \longrightarrow f'(x) = 2x} \\ \large{f'(x) = 2 {x}^(2 - 1) } \\ \large{f'(x) = 2x}`

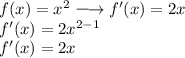
Thus,

`\large{ \int \limits^a_b ( {x}^(2) + 2x)dx} \\ \large{\int \limits^a_b ( (1)/(3) {x}^(3) + {x}^(2)) }`

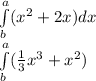
Normally, if it's an indefinite Integral then we'd just put + C after (1/3)x³+x² but since we have a and b, it's a definite Integral.

`\large{ \int \limits^b_a f(x)dx = F(b) - F(a)}`

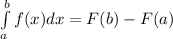
Define F(x) as our anti-diff

From our problem, substitute x = a in then subtract with the one that substitute x = b

`\large{ ((1)/(3){a}^(3) + {a}^(2) ) - ( (1)/(3) {b}^(3) + {b}^(2)) }`

Simplify as we get:

`\large \boxed{ (1)/(3){a}^(3) + {a}^(2) - (1)/(3) {b}^(3) - {b}^(2)}`