Question

The distribution of student scores on the quantitative section of the SATs have an approximately normal distribution with a mean score of 501 points, and a standard deviation of 85 points. If you randomly select one student who has taken the SAT, what is the probability that the student will have scored greater than 600 points on the quantitative section of the SATs

Answer 1

0.122 = 12.2% probability that the student will have scored greater than 600 points on the quantitative section of the SATs.

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

Mean score of 501 points, and a standard deviation of 85 points.

This means that
`\mu = 501, \sigma = 85`

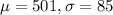
What is the probability that the student will have scored greater than 600 points on the quantitative section of the SATs?

This is 1 subtracted by the p-value of Z when X = 600. So

`Z = (X - \mu)/(\sigma)`

`Z = (600 - 501)/(85)`

`Z = 1.165`

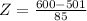
`Z = 1.165` has a p-value of 0.878.

1 - 0.878 = 0.122

0.122 = 12.2% probability that the student will have scored greater than 600 points on the quantitative section of the SATs.