Solution :
a). Applying the energy balance,
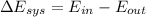
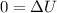
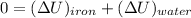
![$0=[mc(T_f-T_i)_(iron)] + [mc(T_f-T_i)_(water)]$](https://img.qammunity.org/2022/formulas/chemistry/college/on7lyj4em49agu6gh0eo4umk5up3dldihh.png)
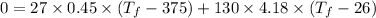
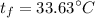
b). The entropy change of iron.
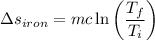
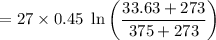
= -9.09 kJ-K
Entropy change of water :
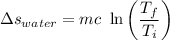
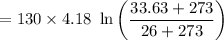
= 10.76 kJ-K
So, the total entropy change during the process is :
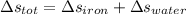
= -9.09 + 10.76
= 1.67 kJ-K
c). Exergy of the combined system at initial state,
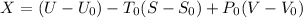
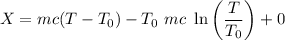

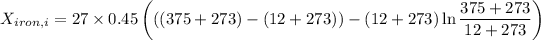

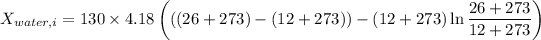
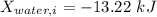
Therefore, energy of the combined system at the initial state is
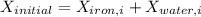
= 63.94 -13.22
= 50.72 kJ
Similarly, Exergy of the combined system at initial state,
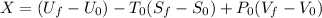
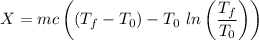
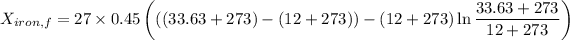
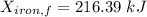
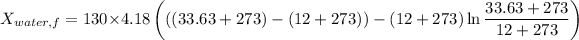
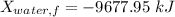
Thus, energy or the combined system at the final state is :
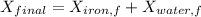
= 216.39 - 9677.95
= -9461.56 kJ
d). The wasted work


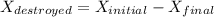
= 50.72 + 9461.56
= 9512.22 kJ