Answer: x ≥ 5
Since x is a natural number, this is the same as saying x > 4
=======================================================
Step-by-step explanation:
Let's solve for x
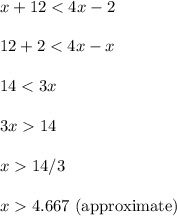
Since
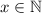 , this means x is a natural number and a value from the set {1,2,3,4,...} aka the set of positive whole numbers. Zero is not in the set of natural numbers.
, this means x is a natural number and a value from the set {1,2,3,4,...} aka the set of positive whole numbers. Zero is not in the set of natural numbers.
So we'll need to round that 4.667 to the nearest whole number to get x ≥ 5
If we were to replace x with anything from the set {5, 6, 7, 8, ...}, then that would make the original inequality to be true.
The notation x ≥ 5 and x > 4 are identical when x is a natural number, because we're describing the same solution set of any whole number 5 or larger.